martes, 20 de marzo de 2012

Pentágono

Un pentágono regular.

En geometría, se denomina pentágono (del griego πεντάγωνον, de πεντά, "cinco" y γωνον, "ángulos") a un polígono de cinco lados y cinco vértices.

"Pentágonos regulares"

Un pentágono regular es aquél que tiene todos sus lados iguales y sus ángulos internos congruentes. Cada ángulo interno mide 108 grados ó $3\pi/5$ radianes. Así, por ejemplo (véase la figura), el ángulo BCD mide 108°. La suma de los ángulos internos de un pentágono regular es de 540° ó $3\pi$ radianes.

Como los segmentos DE, EA, y AB son iguales, los arcos que ellos determinan en la circunferencia circunscrita son iguales. Esto implica que los tres ángulos DCE, ECA y ACB son iguales. Como la suma de ellos es 108°, cada uno de ellos mide 36°.

Cada ángulo externo del pentágono regular mide 72º ó $2\pi/5$ rad.

Área

El área de un pentágono convexo regular de lado a se puede obtener de la siguiente fórmula:

$A = \frac{5a^2}{4}\cot \frac{\pi}{5} = \frac {a^2}{4} \sqrt{25+10\sqrt{5}} \simeq 1,72048 a^2$

De forma general si tenemos que el radio de la circunferencia circunscrita es r_u

$A=\frac{5}{8}\cdot r_u^2 \cdot \sqrt{10+2\sqrt{5}}$

o también:

$A=\frac{5}{2}\cdot r_u^2 \cdot \sin{72^\circ}$

[editar]Perímetro

Siempre que supongamos que el pentágono tiene lado a:

$a=2 \cdot r_u \cdot \cos 54^\circ$

ó también:

$a=r_u \cdot \sqrt{\frac{5 - \sqrt{5}}{2}}$

Para obtener el perímetro P de un pentágono regular, multiplíquese la longitud t de uno de sus lados por cinco (el número de lados n del polígono).

$P = n\cdot t = 5\ t$

[editar]Fórmula para calcular los ángulos interiores:

La suma de todos los ángulos interiores de un pentágono es 540°.

La fórmula general para calcular la suma de los ángulos interiores de cualquier polígono regular (en el caso del pentágono n = 5) es:

$\sum {\alpha =}(n - 2) \cdot 180^\circ = 3 \cdot 180^\circ = 540^\circ$

El ángulo comprendido entre dos lados de un pentágono regular se puede calcular mediante la siguiente fórmula (en el pentágono, n = 5):

$\alpha =\frac{(n - 2)}{n} \cdot 180^\circ = \frac{3}{5} \cdot 180^\circ = 108^\circ$

Algunas aplicaciones trigonométricas:

$\sin \frac{\pi}{10} = \sin 18^\circ = \frac{\sqrt 5 - 1}{4}$

$\cos \frac{\pi}{10} = \cos 18^\circ = \frac{\sqrt{2(5 + \sqrt 5)}}{4}$

$\tan \frac{\pi}{10} = \tan 18^\circ = \frac{\sqrt{5(5 - 2 \sqrt 5)}}{5}$

$\cot \frac{\pi}{10} = \cot 18^\circ = \sqrt{5 + 2 \sqrt 5}$

$\sin \frac{\pi}{5} = \sin 36^\circ = \frac{\sqrt{2(5 - \sqrt 5)} }{4}$

$\cos \frac{\pi}{5} = \cos 36^\circ = \frac{\sqrt 5+1}{4}$

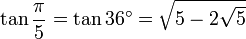
$\tan \frac{\pi}{5} = \tan 36^\circ = \sqrt{5 - 2\sqrt 5}$

$\cot \frac{\pi}{5} = \cot 36^\circ = \frac{ \sqrt{5(5 + 2\sqrt 5)}}{5}$

No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)