Octógono
Octógono u octágono (el DRAE reconoce la validez de ambas formas, pero prefiere "octógono")1 es una figura plana con ocho lados y ocho vértices.

Características
Un octógono tiene 20 diagonales, resultado que se puede obtener aplicando la ecuación general para determinar el número de diagonales de un polígono,  ; siendo el número de lados
; siendo el número de lados  , tenemos:
, tenemos:
 ; siendo el número de lados
; siendo el número de lados  , tenemos:
, tenemos:
La suma de todos los ángulos internos de cualquier octógono es 1080 grados ó  radianes. para el pentogono es P*a/2.A y el perimetro es L+L+L+L+L.P
radianes. para el pentogono es P*a/2.A y el perimetro es L+L+L+L+L.P
 radianes. para el pentogono es P*a/2.A y el perimetro es L+L+L+L+L.P
radianes. para el pentogono es P*a/2.A y el perimetro es L+L+L+L+L.P[editar]Octógono regular
En un polígono regular de ocho lados (octógono regular) sus lados y ángulos son iguales (congruentes) y los lados se unen formando un ángulo de 135º ó  rad. Cada ángulo externo del octógono regular mide 45º ó
rad. Cada ángulo externo del octógono regular mide 45º ó  rad.
rad.
 rad. Cada ángulo externo del octógono regular mide 45º ó
rad. Cada ángulo externo del octógono regular mide 45º ó  rad.
rad.
Para obtener el perímetro P de un octógono regular, multiplíquese la longitud t de uno de sus lados por ocho (el número de lados n del polígono).
pero si solo se conoce la longitud del apotema del polígono,a, el valor del perímetro será:
El área A de un octógono regular de lado t se calcula mediante la fórmula:
Si se conoce la longitud del apotema a del polígono, una alternativa para calcular el área es:
Si sólo conocemos el lado t, podemos calcular el área2 con la siguiente fórmula:
Si sólo conocemos el valor de a, podemos calcular el área:




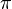 es la constante
es la constante  es la función
es la función 


No hay comentarios:
Publicar un comentario