Decágono
Propiedades
Un decágono tiene 35 diagonales, resultado que se puede obtener aplicando la ecuación general para deteminar el número de diagonales de un polígono,  ; siendo el número de lados
; siendo el número de lados  , tenemos:
, tenemos:
 ; siendo el número de lados
; siendo el número de lados  , tenemos:
, tenemos:[editar]Decágono regular
Un decágono regular, es aquel que tiene sus diez lados de igual longitud y todos los ángulos internos de la misma graduación. Una característica de un decágono regular es que si se inscribe en una circunferencia el lado resulta ser la sección áurea del radio. Los ángulos interiores de un decágono miden 144º ó  rad. Cada ángulo externo del decágono regular mide 36º ó
rad. Cada ángulo externo del decágono regular mide 36º ó  rad.
rad.
 rad. Cada ángulo externo del decágono regular mide 36º ó
rad. Cada ángulo externo del decágono regular mide 36º ó  rad.
rad.
El perímetro P de un decágono regular puede calcularse multiplicando la longitud t de uno de sus lados por diez (el número de lados n del polígono).
El área A de un decágono regular de lado t se puede calcular de la siguiente manera:
Si se conoce la longitud de la apotema a del polígono, otra alternativa para calcular el área es:





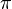 es la constante
es la constante  es la función
es la función 

 , tenemos:
, tenemos:

 rad. Cada
rad. Cada  rad.
rad.



 , tenemos:
, tenemos:

 rad. Cada
rad. Cada  rad.
rad.






 , tenemos:
, tenemos:




